January – 2025
A flexible class of priors for orthonormal matrices with basis function-specific structure
bayesian singular value decomposition
Joshua North
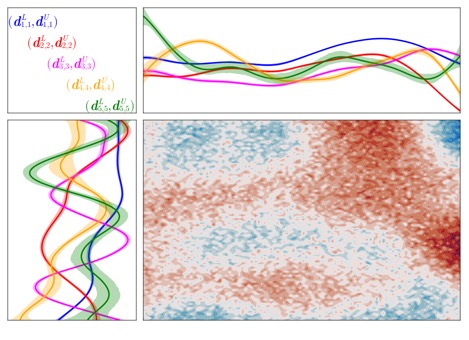
Example of our method applied to singular value decomposition using simulated data (bottom right) that has column (e.g., spatial) and row (e.g., temporal) dependence . The mean (solid lines) and 95% uncertainty bound (shaded region) for the left- (bottom left) and right- (top right) singular vectors and an example of the singular values (top left), which are estimated from the simulated data, are shown.
The Science
In climate science, data is often measured in both space and time. To extract meaningful patterns in the data, scientists often rely on mathematical methods to decompose the data. This manuscript proposes a new method of decomposing the data within a statistical framework. Importantly, the method accounts the spatial and temporal structure of the data and provides estimates of the uncertainty about those structures. The method is applied to two-meter air temperature data from the Pacific Northwest, enhancing our understanding of the Earth system’s internal variability.
The Impact
Traditional mathematical methods used to decompose climate data do not account for uncertainty in the method or the data and do not respect the spatial and temporal structure of the data. Our approach addresses all of these issues by proposing a statistical method of modeling the decomposition. This is particularly useful for climate science where understanding spatial patterns and trends with confidence is crucial. Additionally, our method allows a scientist to incorporate prior knowledge of the system into the decomposition, which aids in the interpretability and accuracy of the models.
Summary
In climate science, where data are spatially- and temporally-oriented, scientists often rely on matrix decomposition methods, such as singular value decomposition (SVD), to extract meaningful patterns. However, the basis functions in these factorizations are typically computed using algorithmic methods that cannot quantify uncertainty or account for
basis function correlation structure before estimation. This manuscript proposes a new prior distribution for matrices arising from matrix decomposition methods that can explicitly model basis function-specific structure. The prior is used within a general probabilistic model for SVD to conduct posterior inference on the basis functions while accounting for measurement error and fixed effects. The prior specification can be used for various scenarios and has favorable model properties as demonstrated through synthetic data examples. The method is applied to two-meter air temperature data from the Pacific Northwest, enhancing our understanding of the Earth system’s internal variability.
Contact
Joshua North, jsnorth@lbl.gov
Lawrence Berkeley National Laboratory, Climate and Ecosystem Sciences Division
Mark Risser, mdrisser@lbl.gov
Lawrence Berkeley National Laboratory, Climate and Ecosystem Sciences Division
Funding
● Director, Office of Science, Office of Biological and Environmental Research of the U.S. Department of Energy, USA under Contract No. DE-AC02-05CH11231
● Regional and Global Model Analysis Program area within the Earth and Environmental Systems Modeling Program, USA
● National Science Foundation, USA [OAC-1931363, ACI-1553685]
● National Institute of Food & Agriculture, USA [COL0-FACT-2019]
● National Energy Research Scientific Computing Center (NERSC)
● Office of Science of the U.S. Department of Energy, under Contract No. DE-AC02-05CH11231.
Publications
Joshua S. North, Mark D. Risser, F. Jay Breidt, A flexible class of priors for orthonormal matrices with basis function-specific structure, Spatial Statistics, Volume 64, 2024, 100866, [DOI: https://doi.org/10.1016/j.spasta.2024.100866]
